51. If each edge of a cube is increased by 50%, find the percentage increase in its surface area.
Sol: Let the original length of each edge = a
Then, Original surface area = 6a^2
New surface area = 6 * (3a/2)^2 = 27a^2/2
Increase percent in surface area = (15/2a^2 * 1/(6a^2) * 100)% = 125%
52. Find the number of the bricks, each measuring 25 cm by 12.5 cm by 7.5 cm, required to build a wall 6 m long, 5 m high and 50cm thick, while the mortar occupies 5% of the volume of the wall.
Sol: Volume of the Wall = (600 * 500 * 50) cu. Cm.
Volume of the bricks = 95% of the volume of the wall.
= (95/100 * 600 * 500 * 50) cu. Cm.
Volume of 1 brick = (25 * 25/2 * 75/2) cu. Cm.
Therefore, Number of bricks = (95/100 * (600 * 500 * 50 * 2 * 10)/(25 * 25 * 75))=6080
53. The base of a triangular field is three times its altitude. If the cost of cultivating the field at Rs. 24.68 per hectare be Rs. 333.18, find its base and height.
Sol: Area of the field = Total cost/Rate = (333.18/24.68) hectares =13.5 hectares.
= (13.5*10000) m^2 =135000m^2.
Let altitude = x meters and base = 3x meters.
Then, ½ *3x* x= 135000 or x^2 = 9000 or x= 300.
Therefore, base =900 m & altitude = 300m.
54. Find the area of a rhombus one side of which measures 20cm and one diagonal
24cm.
Sol: Let, other diagonal = 2x cm,
Since halves of diagonals and one side of rhombus form a right angled triangle
with side as hypotenuse, we have:
(20)^2 =(12)^2+x^2 or x=Ö(20)^2-(12)^2 =Ö256=16 cm.
Therefore, other diagonal = 32 cm.
55. A tank is fitted with 8 pipes, some of them that fill the tank and others that are waste pipe meant to empty the tank. Each of the pipes that fill the tank can fill it in 8 hours, while each of those that empty the tank can empty it in 6 hours. If all the pipes are kept open when the tank is full, it will take exactly 6 hours for the tank to empty. How many of these are fill pipes?
Sol. Let the number of fill pipes be 'n'. Therefore, there will be 8-n, waste pipes.
Each of the fill pipes can fill the tank in 8 hours. Therefore, each of the fill pipes will fill 1/8th
of the tank in an hour.
Hence, n fill pipes will fill n/8th of the tank in an hour.
Similarly, each of the waste pipes will drain the full tank in 6 hours. That is, each of the
waste pipes will drain 1/6th of the tank in an hour.
Therefore, (8-n) waste pipes will drain ((8-n)/6)th of the tank in an hour.
Between the fill pipes and the waste pipes, they drain the tank in 6 hours. That is, when all
8 of them are opened, 1/6th of the tank gets drained in an hour.
(Amount of water filled by fill pipes in 1 hour - Amount of water drained by waste pipes 1
hour)
= 1/6th capacity of the tank drained in 1 hour.
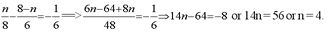
56. A pump can be used either to fill or to empty a tank. The capacity of the tank is 3600 m3. The emptying capacity of the pump is 10 m3/min higher than its filling capacity. What is the emptying capacity of the pump if the pump needs 12 more minutes to fill the tank than to empty it?
Sol. Let 'f' m3/min be the filling capacity of the pump. Therefore, the emptying capacity of the
pump will be = (f + 10 ) m3 / min.
The time taken to fill the tank will be = 
minutes
And the time taken to empty the tank will be = 
.
We know that it takes 12 more minutes to fill the tank than to empty it
i.e 
=> 3600 f + 36000 - 3600 f = 12 (f2 + 10 f)
=> 36000 = 12 (f2 + 10 f) => 3000 = f2 + 10 f => f2 + 10 f - 3000 = 0.
Solving for positive value of 'f' we get, f = 50.
Therefore, the emptying capacity of the pump = 50 + 10 = 60 m3 / min
57. X alone can do a piece of work in 15 days and Y alone can do it in 10 days. X and Y undertook to do it for Rs. 720. With the help of Z they finished it in 5 days. How much is paid to Z?
Sol. In one day X can finish 1/15th of the work.
In one day Y can finish 1/10th of the work.
Let us say that in one day Z can finish 1/Zth of the work.
When all the three work together in one day they can finish 1/15 + 1/10 + 1/Z = 1/5th of the
work.
Therefore, 1/Z = 1/30.
Ratio of their efficiencies = 1/15: 1/10: 1/30 = 2: 3: 1.Therefore Z receives 1/6th of the total
money.
According to their efficiencies money is divided as 240: 360: 120.
Hence, the share of Z = Rs. 120.
58. Pipe A usually fills a tank in 2 hours. On account of a leak at the bottom of the tank, it takes pipe A 30 more minutes to fill the tank. How long will the leak take to empty a full tank if pipe A is shut?
Ans:10 hours
Sol. Pipe A fills the tank normally in 2 hours. Therefore, it will fill ½ of the tank in an hour.
Let the leak take x hours to empty a full tank when pipe A is shut. Therefore, the leak will
empty 
of the tank in an hour.
The net amount of water that gets filled in the tank in an hour when pipe A is open and when
there is a leak =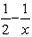 
of the tank. — (1)
When there is a leak, the problem states that Pipe A takes two and a half hours to fill the tank. i.e.
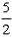hours. Therefore, in an hour, 
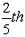of the tank gets filled. – (2)
Equating (1) and (2), we get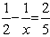 
=> 
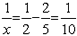=> x = 10 hours.
The problem can also be mentally done as follows.
Pipe A takes 2 hours to fill the tank. Therefore, it fills half the tank in an hour or 50%
of the tank in an hour.
When there is a leak it takes 2 hours 30 minutes for the tank to fill. i.e 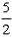hours to fill the
tank or 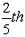or 40% of the tank gets filled.
On account of the leak, (50 - 40)% = 10% of the water gets wasted every hour.
Therefore, the leak will take 10 hours to drain a full tank.
59. How many number of times will the digit '7' be written when listing the integers from 1 to 1000?
Sol:7 does not occur in 1000. So we have to count the number of times it appears between 1 and
999. Any number between 1 and 999 can be expressed in the form of xyz where 0 < x, y, z < 9.
1. The numbers in which 7 occurs only once. e.g 7, 17, 78, 217, 743 etc
This means that 7 is one of the digits and the remaining two digits will be any of the other
9 digits (i.e 0 to 9 with the exception of 7)
You have 1*9*9 = 81 such numbers. However, 7 could appear as the first or the second
or the third digit. Therefore, there will be 3*81 = 243 numbers (1-digit, 2-digits and 3-
digits) in which 7 will appear only once.
In each of these numbers, 7 is written once. Therefore, 243 times.
2. The numbers in which 7 will appear twice. e.g 772 or 377 or 747 or 77
In these numbers, one of the digits is not 7 and it can be any of the 9 digits ( 0 to 9 with
the exception of 7).
There will be 9 such numbers. However, this digit which is not 7 can appear in the first
or second or the third place. So there are 3 * 9 = 27 such numbers.
In each of these 27 numbers, the digit 7 is written twice. Therefore, 7 is written 54 times.
3. The number in which 7 appears thrice - 777 - 1 number. 7 is written thrice in it.
Therefore, the total number of times the digit 7 is written between 1 and 999 is 243 + 54
+ 3 = 300
60. There are 5 Rock songs, 6 Carnatic songs and 3 Indi pop songs. How many different albums can be formed using the above repertoire if the albums should contain at least 1 Rock song and 1 Carnatic song?
Sol: There are 2n ways of choosing 'n' objects. For e.g. if n = 3, then the three objects can be
chosen in the following 23 ways - 3C0 ways of choosing none of the three, 3C1 ways of
choosing one out of the three, 3C2 ways of choosing two out of the three and 3C3 ways of
choosing all three.
In the given problem, there are 5 Rock songs. We can choose them in 25 ways. However, as
the problem states that the case where you do not choose a Rock song does not exist (at
least one rock song has to be selected), it can be done in 25 - 1 = 32 - 1 = 31 ways.
Similarly, the 6 Carnatic songs, choosing at least one, can be selected in 26 - 1 = 64 - 1 =
63 ways.
And the 3 Indi pop can be selected in 23 = 8 ways. Here the option of not selecting even
one Indi Pop is allowed.
Therefore, the total number of combinations = 31 * 63 * 8 = 15624
